-
摘要:
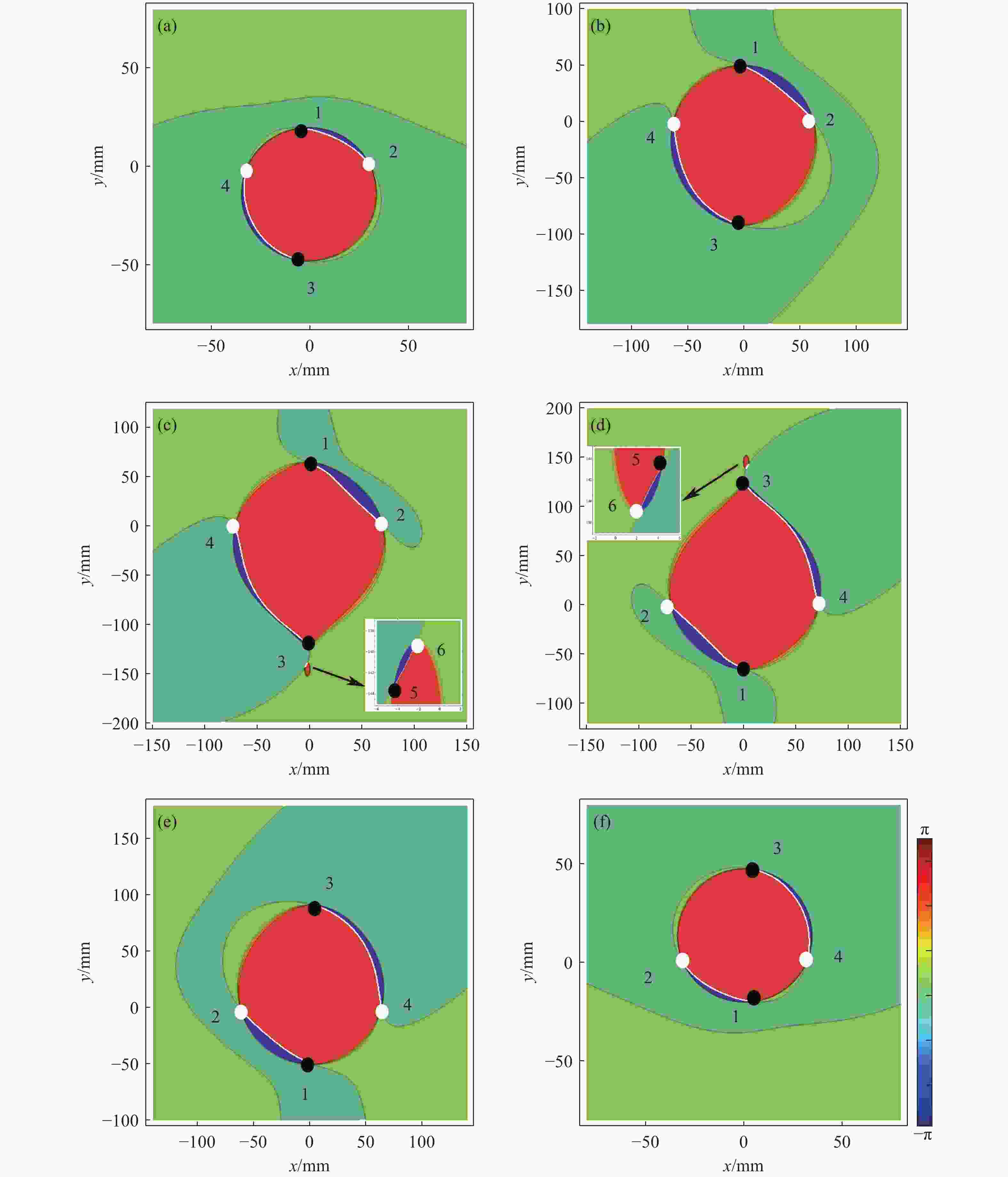
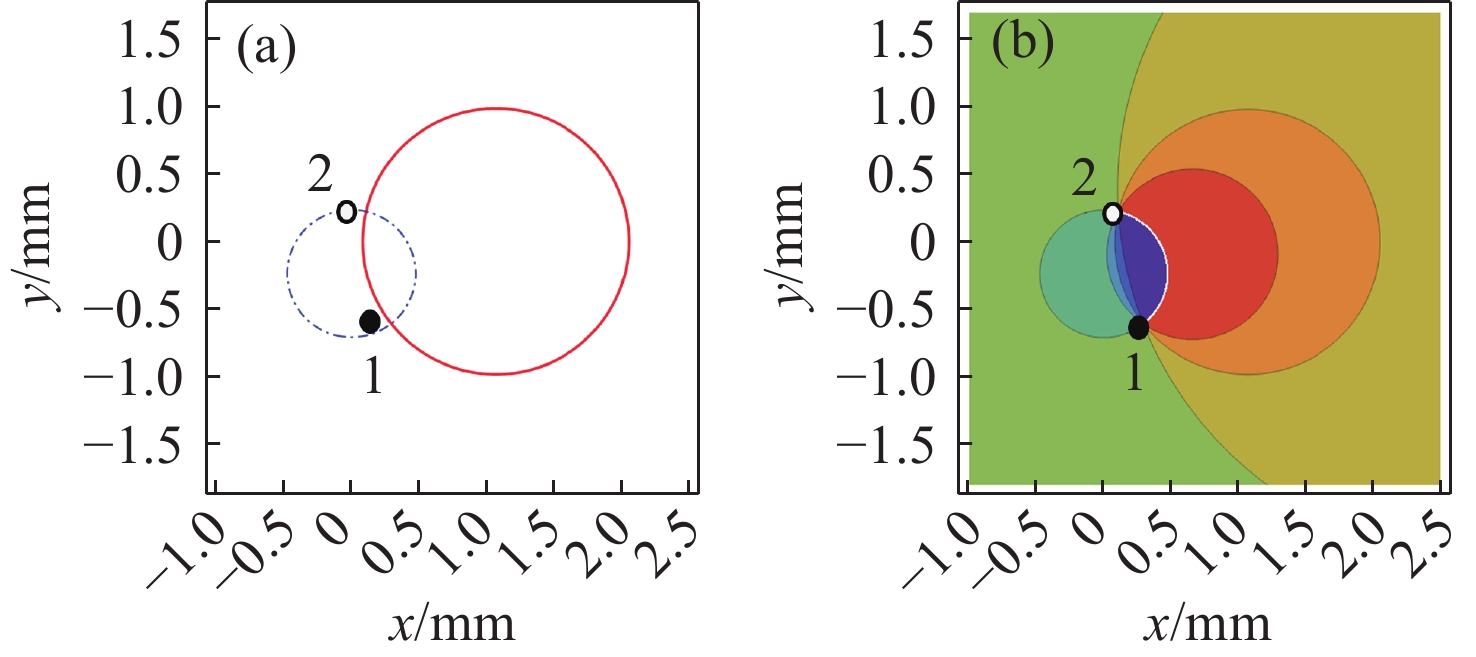
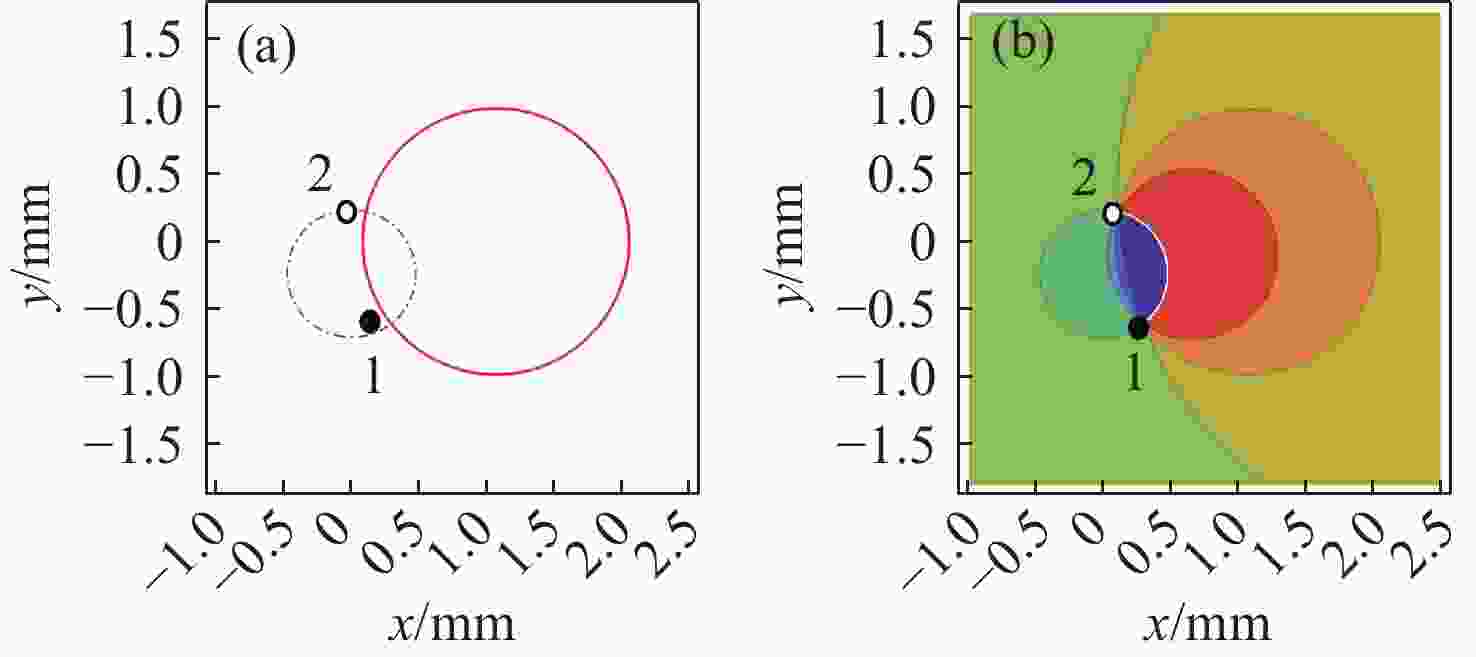
目的: 为探究寄存于部分相干矢量光束的C点偶极子海洋湍流中演化规律,构建了C点偶极子的高斯-谢尔模涡旋(GSMV)光束,并据此对C点偶极子在海洋湍流中演化行为进行研究。方法: 根据部分相干矢量光束偏振奇点概念,构造了GSMV光束,实现部分相干光束携带一对带相反拓扑电荷C点偶极子。再根据扩展惠更斯-菲涅耳原理和数学积分公式,推导出携带C点偶极子的GSMV光束通过海洋湍流的谱密度表示式。最后运用该表达式以及复斯托克斯场S 12 =S 1 + iS 2等相位图,模拟计算并分析讨论光束传播距离z、光束初始离轴参数s 与相干长度δ 对C点偶极子海洋湍流中演化行为影响。结果: 当GSMV光束传输时,构成偶极子的C点位置和偏振度均会变化。当参数s 、δ 或z 变化时,虽然有新的C点产生,也有带相反拓扑电荷的C点发生湮没,但光场中偏振奇点总的拓扑电荷保持守恒。结论: 携带C点偶极子的部分相干矢量光束在海洋湍流中传输时,该光束的离轴参数、相干长度、湍流强度或传输距离对C点偶极子演化均有影响。Abstract:Objetive: In order to find out performance of the C-point dipole nested in partially coherent stochastic vortex beam in oceanic turbulence, the Gaussian-Schell model vortex (GSMV) beam carrying a C-point dipole is constructed, which is used to find out the evolution property of the C-point dipole in oceanic turbulence. Method: According to the definition of the polarization singularities from partially coherent vector beams, the GSMV beam carrying a C-point dipole is constructed. According to the extended Huygens–Fresnel principle, the formula of the cross-spectral density (CSD) for the GSMV beam propagating through oceanic turbulence is deduced by use of the integral formula. In accordance with the formula of the CSD derived above, the effects of propagation distance
z , the off-axis parameters and coherent lengthδ on the evolution behavior of the C-point dipole is illustrated and analyzed. The position of a C point can be determined by the contour lines of phase of Stokes fieldS 12 =S 1 + iS 2. The degree of polarization of a C point can be calculated by spectral Stokes parameters, while its topological charge can be judged by the sign principle which was proposed by Freund. Result: It is shown that, the position and the degree of polarization of the C points may be changed with propagation of the host beam. Though the creation and annihilation of C points may occur with variation of the propagation distance, the total of the topological charges of C points of the beam hold consistent. Besides, as the off-axis parameters are chosen as opposite numbers, the numbers of C points from the optical fields are equal. Conclusion: when the partially coherent vortex beam carrying a C-point dipole propagates in oceanic turbulence, the evolution behavior of the C-point dipole is affected by the propagation distance of the host beam, the off-axis parameter, turbulence intensity as well as the spatial coherent length.-
Key words:
- Singular optics /
- polarization singularities /
- C point /
- oceanic turbulence
-
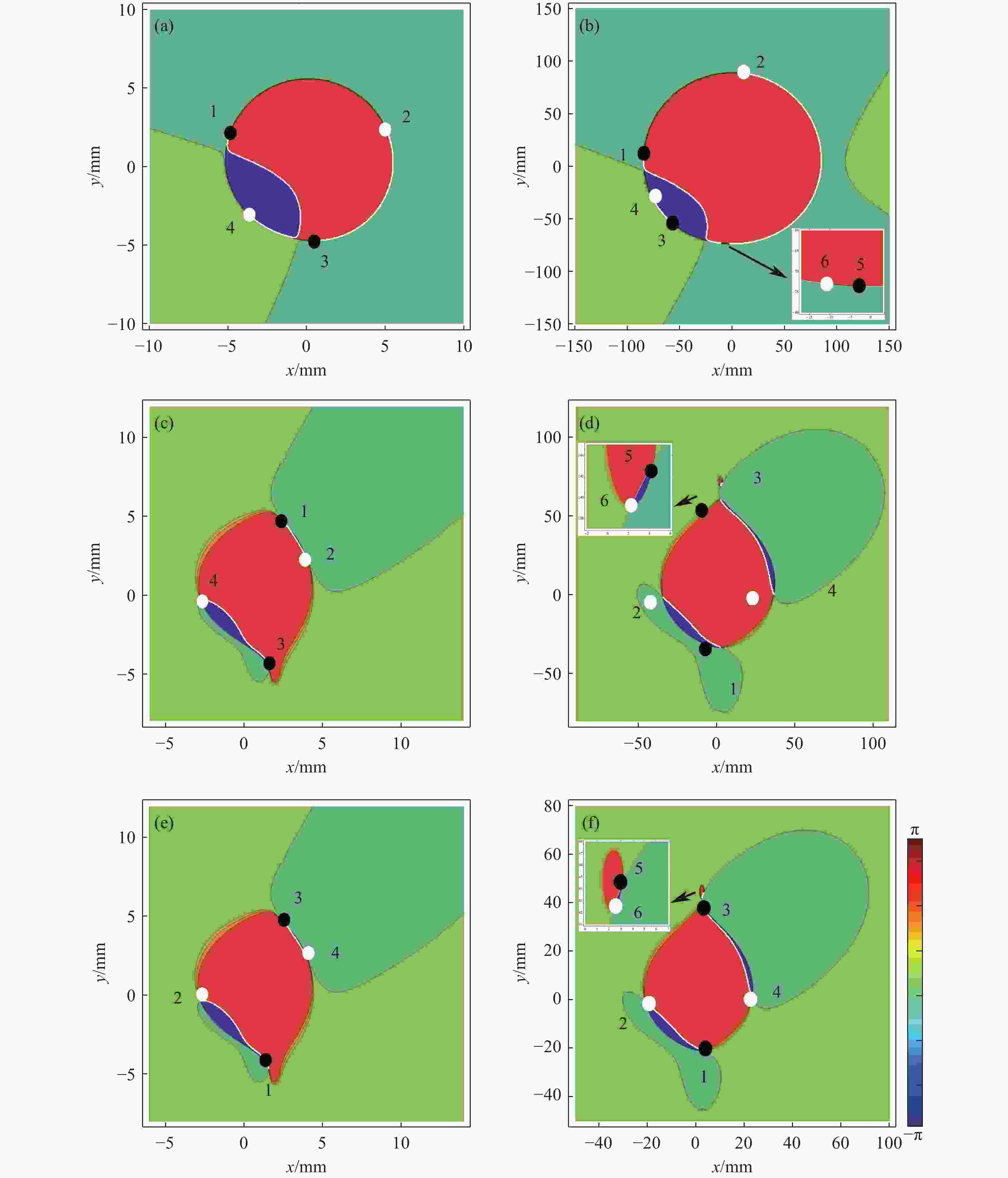
图 4 海洋湍流中GSMV光束在不同湍流强度和相干长度情形下的 S12 相位分布。(a) T = 1.18×10−12, δxx = 0.03 mm, z = 5 m;(b) T = 1.18×10−12, δxx = 0.03 mm, z = 80 m;(c) T = 1.18×10−12, δxx = 0.15 mm, z = 5 m;(d) T = 1.18×10−12, δxx = 0.15 mm, z = 50 m;(e) T = 1.18×10−11, δxx = 0.15 mm, z = 5 m;(f) T = 1.18×10−11, δxx = 0.15 mm, z = 30 m
Figure 4. Contour lines of phase of S12 for GSMV beam for different values of theturbulence intensity and coherent length. (a) T = 1.18×10−12, δxx = 0.03 mm, z = 5 m; (b) T = 1.18×10−12, δxx = 0.03 mm, z = 80 m; (c) T = 1.18×10−12, δxx = 0.15 mm, z = 5 m; (d) T = 1.18×10−12, δxx = 0.15 mm, z = 50 m; (e) T = 1.18×10−11, δxx = 0.15 mm, z = 5 m; (f) T = 1.18×10−11, δxx = 0.15 mm, z = 30 m
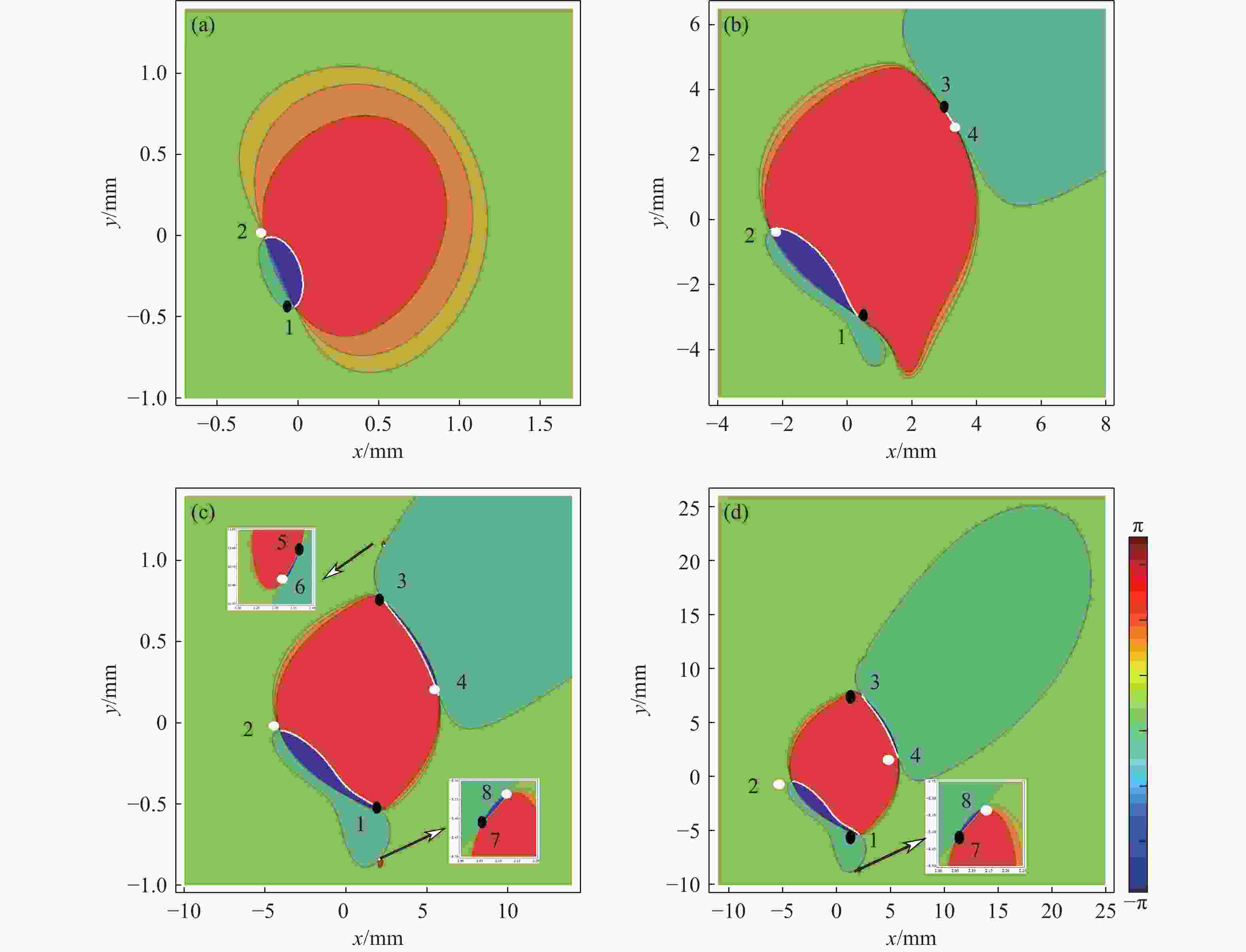
图 3 GSMV光束海洋湍流中不同离轴参数 s 的 S12等相位图。 (a) s = −0.8 mm;(b) s = −0.46 mm;(c) s = −0.41 mm; (d) s = 0.41 mm; (e) s = 0.46 mm; (f) s = 0.8 mm
Figure 3. Contour lines of S12 for the GSMV beam with different off-axis parameter. (a) s = −0.8 mm; (b) s = −0.46 mm; (c) s = −0.41 mm; (d) s = 0.41 mm; (e) s = 0.46 mm; (f) s = 0.8 mm
-
[1] NYE J F, HAJNAL J V. The wave structure of monochromatic electromagnetic radiation[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1987, 409(1836): 21-36. [2] BERRY M V, DENNIS M R. Polarization singularities in isotropic random vector waves[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2001, 457(2005): 141-155. doi: 10.1098/rspa.2000.0660 [3] DENNIS M R, O'HOLLERAN K, PADGETT M J. Singular optics: optical vortices and polarization singularities[J]. Progress in Optics, 2009, 53: 293-363. [4] KOROTKOVA O, WOLF E. Generalized stokes parameters of random electromagnetic beams[J]. Optics Letters, 2005, 30(2): 198-200. doi: 10.1364/OL.30.000198 [5] YAN H W, LÜ B D. Spectral Stokes singularities of stochastic electromagnetic beams[J]. Optics Letters, 2009, 34(13): 1933-1935. doi: 10.1364/OL.34.001933 [6] YAN H W, LÜ B D. Propagation of spectral Stokes singularities of stochastic electromagnetic beams through atmospheric turbulence[J]. Applied Physics B, 2010, 99(4): 809-815. doi: 10.1007/s00340-009-3892-2 [7] HUANG Y P, ZHANG B, GAO Z H, et al. Evolution behavior of Gaussian Schell-model vortex beams propagating through oceanic turbulence[J]. Optics Express, 2014, 22(15): 17723-17734. doi: 10.1364/OE.22.017723 [8] XU J, ZHAO D M. Propagation of a stochastic electromagnetic vortex beam in the oceanic turbulence[J]. Optics & Laser Technology, 2014, 57: 189-193. [9] LIU D J, YIN H M, WANG G Q, et al. Propagation of partially coherent Lorentz–Gauss vortex beam through oceanic turbulence[J]. Applied Optics, 2017, 56(31): 8785-8792. doi: 10.1364/AO.56.008785 [10] LI Y, ZHANG Y X, ZHU Y. Probability distribution of the orbital angular momentum mode of the ultrashort Laguerre-Gaussian pulsed beam propagation in oceanic turbulence[J]. Results in Physics, 2018, 11: 698-705. doi: 10.1016/j.rinp.2018.10.013 [11] SUN CH, LV X, MA B B, et al. Statistical properties of partially coherent radially and azimuthally polarized rotating elliptical Gaussian beams in oceanic turbulence with anisotropy[J]. Optics Express, 2019, 27(8): A245-A256. doi: 10.1364/OE.27.00A245 [12] LIU D J, WANG G Q, YIN H M, et al. Propagation properties of a partially coherent anomalous hollow vortex beam in underwater oceanic turbulence[J]. Optics Communications, 2019, 437: 346-354. doi: 10.1016/j.optcom.2019.01.006 [13] WANG H, LI H, ZHOU Y L. Research on the influence of anisotropic ocean on the capacity of vortex Hankel–Bessel beam[J]. Optical Engineering, 2022, 61(4): 046102. [14] XU Y G, XU Q, LIU W L. Effect of oceanic turbulence on the propagation behavior of a radially polarized Laguerre–Gaussian Schell-model vortex beam[J]. Journal of the Optical Society of America A, 2023, 40(10): 1895-1907. doi: 10.1364/JOSAA.494951 [15] WANG X G, CHEN M K, YUAN Q J, et al. Transmission characteristics of partially coherent pin-like optical vortex beams in oceanic turbulence[J]. Physica Scripta, 2024, 99(6): 065550. doi: 10.1088/1402-4896/ad497e [16] YE F, ZHANG J B, DENG D M, et al. Propagation properties of the rotating elliptical chirped Gaussian vortex beam in the oceanic turbulence[J]. Optics Communications, 2018, 426: 456-462. doi: 10.1016/j.optcom.2018.05.077 [17] LI J H, ZENG J. Dynamic evolution of coherent vortex dipole in atmospheric turbulence[J]. Optics Communications, 2017, 383: 341-348. doi: 10.1016/j.optcom.2016.09.031 [18] FREUND I. Polarization singularity indices in Gaussian laser beams[J]. Optics Communications, 2002, 201(4-6): 251-270. doi: 10.1016/S0030-4018(01)01725-4 [19] FREUND I, MOKHUN A I, SOSKIN M S, et al. Stokes singularity relations[J]. Optics Letters, 2002, 27(7): 545-547. doi: 10.1364/OL.27.000545 [20] FREUND I, SHVARTSMAN N. Wave-field phase singularities: the sign principle[J]. Physical Review A, 1994, 50(6): 5164-5172. doi: 10.1103/PhysRevA.50.5164 [21] KOROTKOVA O, FARWELL N. Polarization changes in stochastic electromagnetic beams propagating in the oceanic turbulence[J]. Proceedings of SPIE, 2010, 7588: 75880S. doi: 10.1117/12.846740 [22] KOROTKOVA O, FARWELL N, SHCHEPAKINA E. Light scintillation in oceanic turbulence[J]. Waves in Random and Complex Media, 2012, 22(2): 260-266. doi: 10.1080/17455030.2012.656731 [23] GRADSHTEYN I S, RYZHIK I M. Table of Integrals, Series, and Products[M]. 7th ed. Burlington: Academic Press, 2007. -





 下载:
下载: