Two-dimensional grating line parameter calibration based on biaxial phase mapping
doi: 10.37188/CO.EN-2025-0020
-
摘要:
二维光栅是平面光栅干涉仪实现高精度、多维位移测量的核心器件，其刻线密度和栅线正交性误差的检测与标校，一方面可提高光栅干涉仪的定位精度，另一方面可为二维光栅的制作提供反馈指导。本文提出一种利用正交外差金宝搏188软件怎么用 干涉仪同时标定二维光栅刻线密度和栅线正交性误差的方法，以待测光栅搭建二维光栅干涉仪，双轴金宝搏188软件怎么用 干涉仪为其提供位移参考，建立光栅干涉与金宝搏188软件怎么用 干涉的相位映射关系，通过任意两次位移获取的干涉相位信息，即可同时解算上述3项参数的同时获取光栅安装误差。使用1200 gr/mm的二维光栅验证了提出方法的可行性，X、Y方向刻线密度的标准差分别为0.012 gr/mm和0.014 gr/mm，栅线正交性误差的标准差为0.004°，安装误差标准差为0.002°。与原子力显微镜法进行了精度比对，X、Y方向刻线密度的一致性优于0.03 gr/mm、0.06 gr/mm，正交性误差优于0.008°。实验结果表明，提出方法可简单、高效的应用于二维光栅的栅线参数标定。
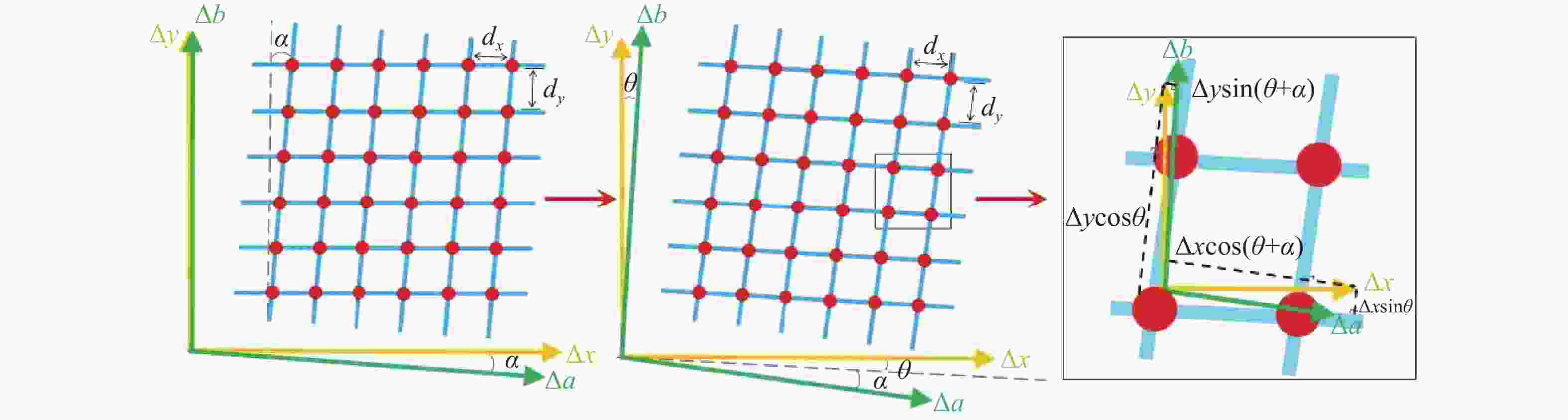
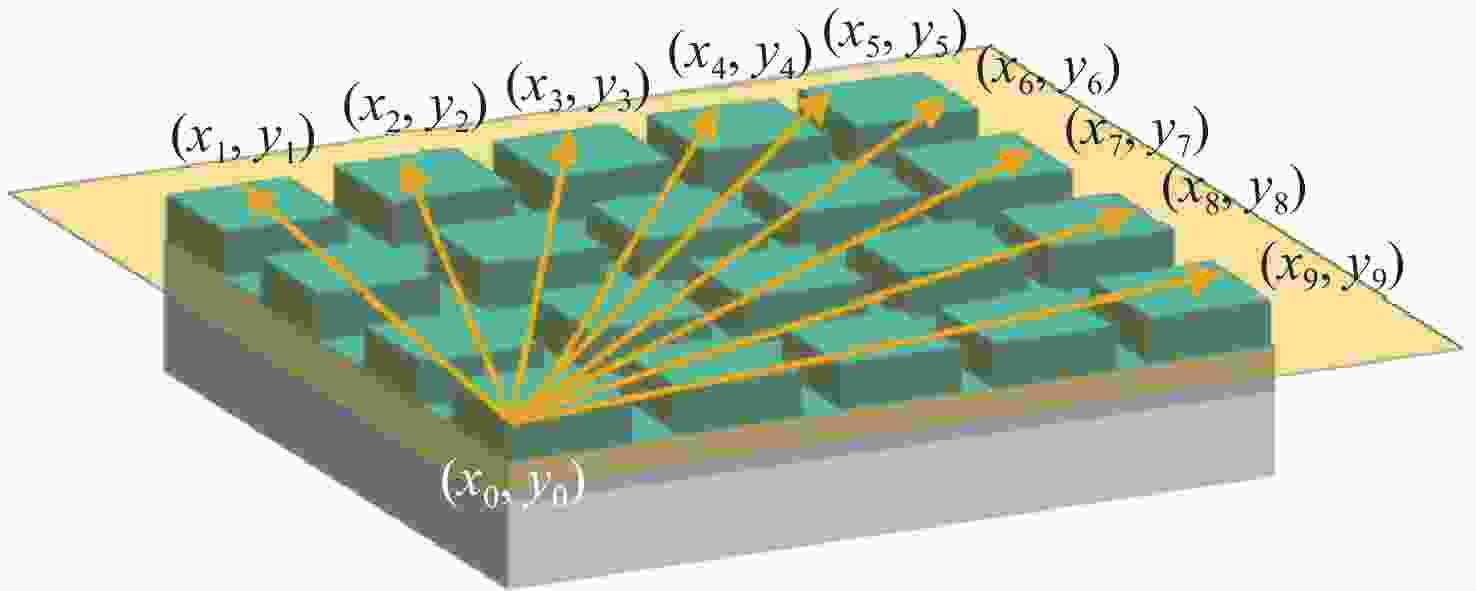
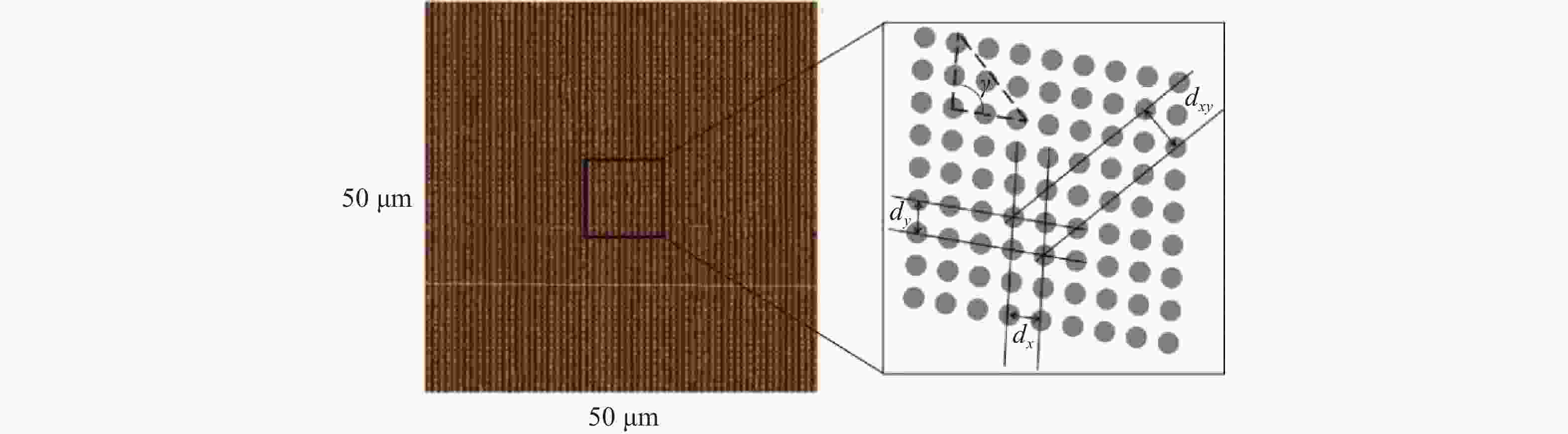
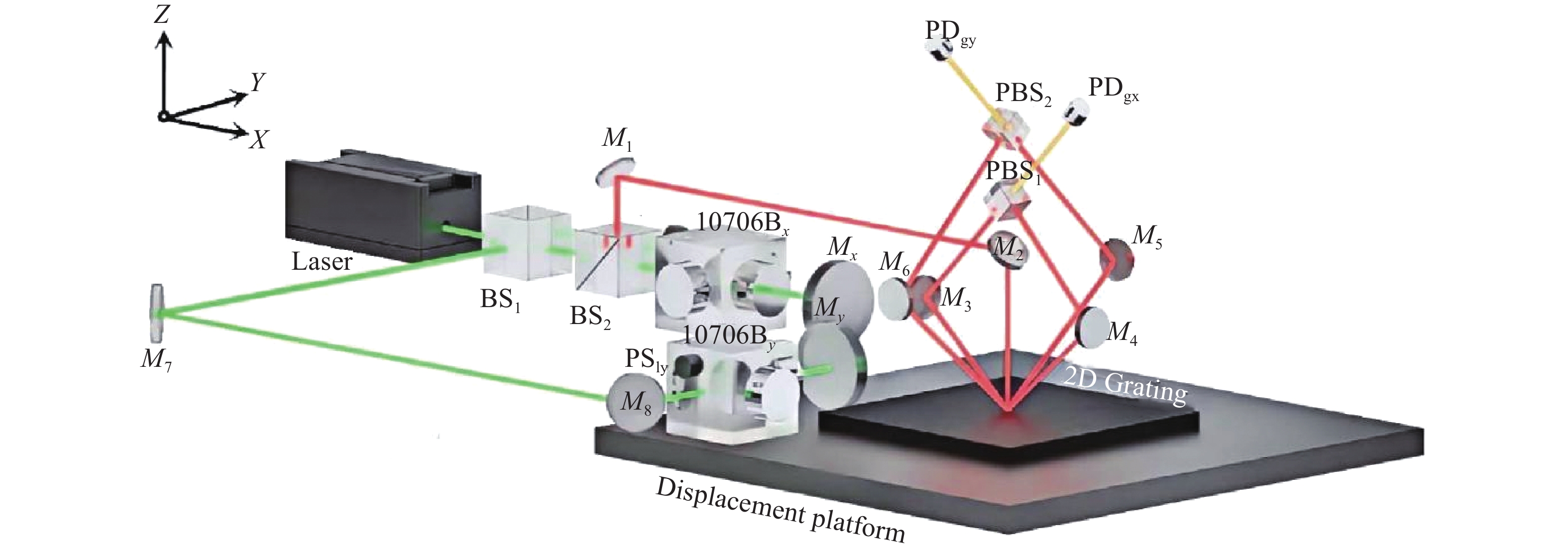
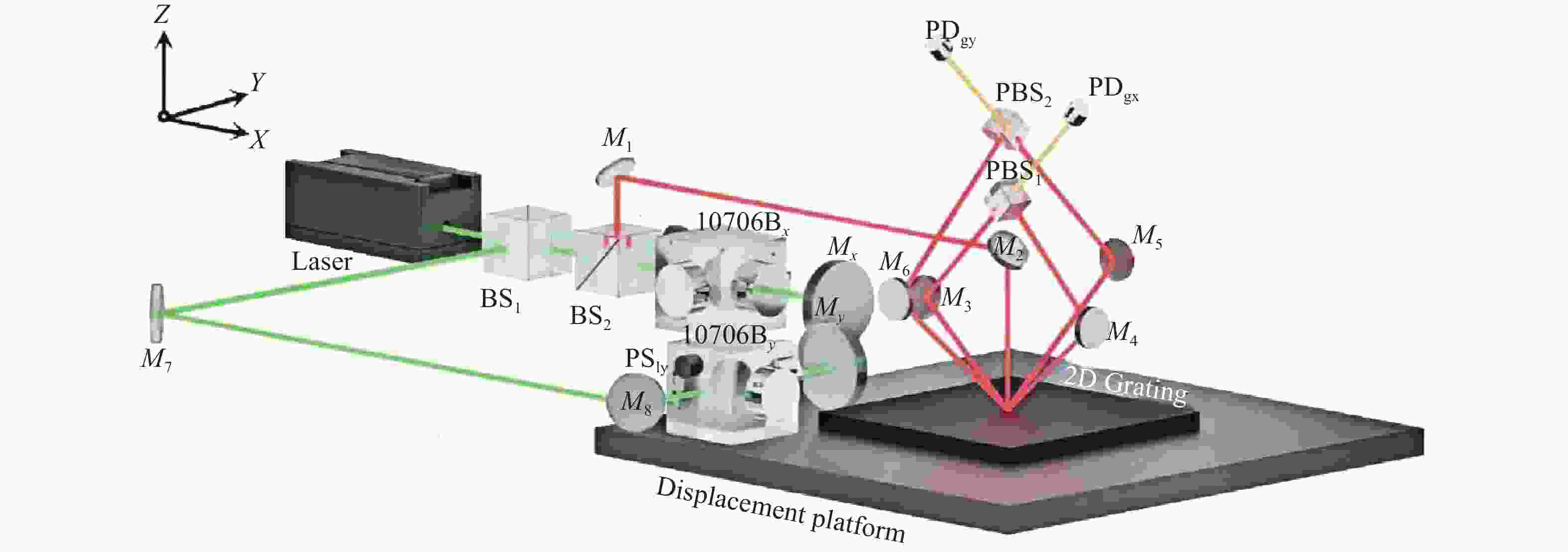
Abstract:The two-dimensional grating serves as a critical component in plane grating interferometers for achieving high-precision multidimensional displacement measurements. The calibration of grating groove density and orthogonality error of grating grooves not only improves the positioning accuracy of grating interferometers but also provides essential feedback for optimizing two-dimensional grating fabrication. This study proposes a method for simultaneous calibration of these parameters using orthogonal heterodyne laser interferometry. A two-dimensional grating interferometer is built with the grating to be measured, and a biaxial laser interferometer provides a displacement reference for it. The phase mapping relationship between grating interference and laser interference is established. The interference phase information obtained by any two displacements can simultaneously solve the above three parameters and obtain the grating installation error. The feasibility of the proposed method is verified by using a 1200 gr/mm two-dimensional grating. The standard deviation of the grating groove density in the X and Y directions is 0.012 gr/mm and 0.014 gr/mm, respectively. The standard deviation of the orthogonality error of grating grooves is 0.004°, and the standard deviation of the installation error is 0.002°. Compared with the atomic force microscope method, the consistency of the grating groove density in the X and Y directions is better than 0.03 gr/mm and 0.06 gr/mm, and the orthogonality error of grating grooves is better than 0.008°. The experimental results show that the proposed method can be simply and efficiently applied to the calibration of the grating line parameters of the two-dimensional grating.
-
Figure 1. The schematic diagram of the optical path structure of the calibration system
Figure 2. The influence of orthogonality error of grating grooves error and grating installation error on displacement measurement
Figure 3. Experimental device photographs. (a) Layout of the 2D grating interferometer. (b) Layout of the laser interferometer. (c) 2D grating.
Figure 4. Stability test result diagrams. (a) Values measured by the X-direction laser interferometer. (b) Values measured by the Y-direction laser interferometer. (c) Measured values from the X-direction grating interferometer. (d) Measured values from the Y-direction grating interferometer.
Figure 5. Linear fitting data diagrams. (a) Results for plane displacement platform movement along the X-axis. (b) Results for plane displacement platform movement along the Y-axis.
Figure 8. Data solution result diagrams. (a) Grating installation error results. (b) Orthogonality error results for the grating lines. (c) X-direction grating groove density results. (d) Y-direction grating groove density results.
Figure 9. The AFM image and data acquisition schematic diagram of 2D grating (a)Measured images of AFM (b) Data acquisition schematic diagram
Figure 10. Comparison of results for the two measurement methods. (a) Comparison of grating groove density measurement results. (b) Comparison of orthogonality error of grating grooves error results.
Table 1. The solution results of the parameters to be measured
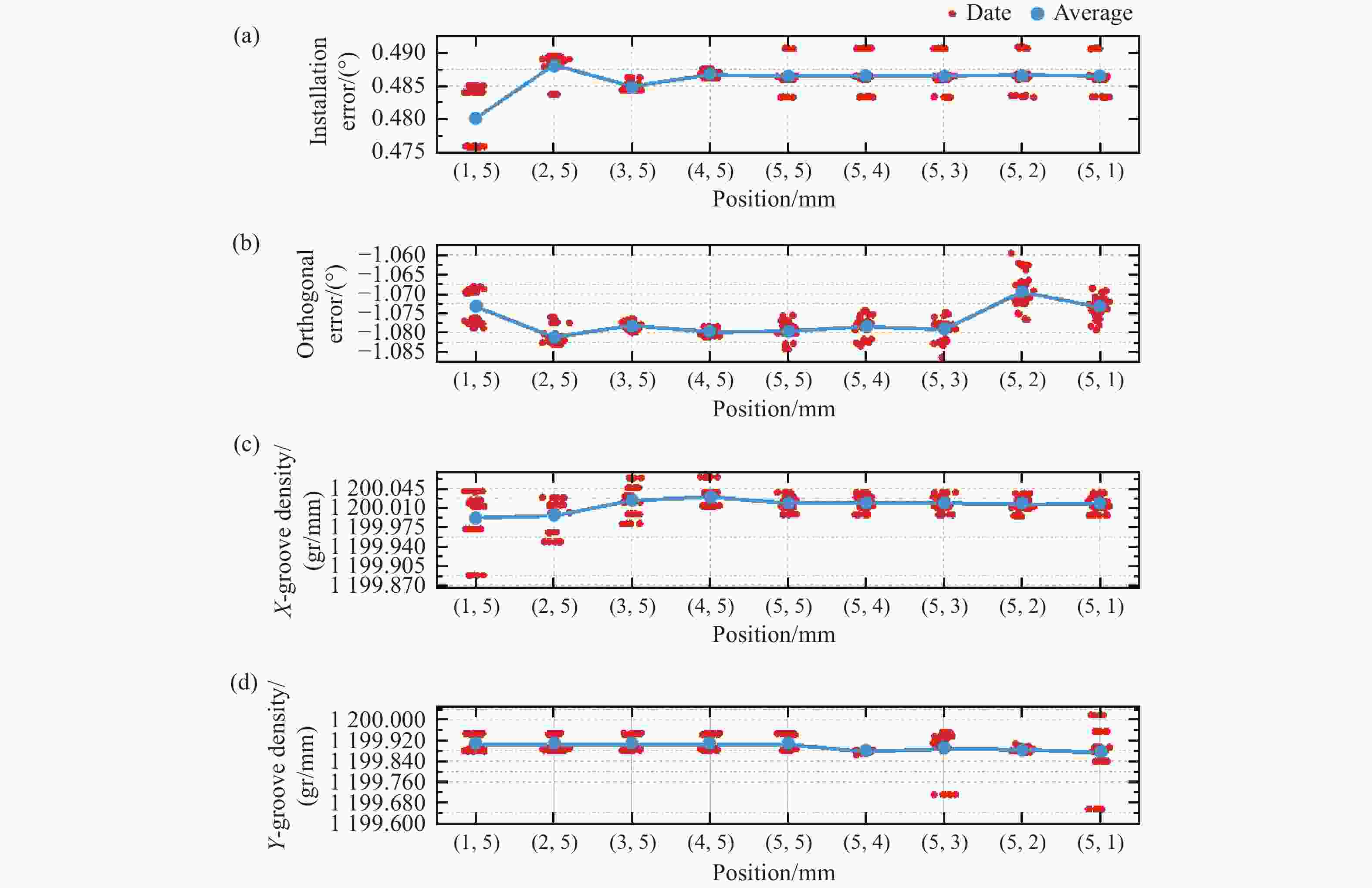
（xn,yn） θ(°) α(°) $ \rho $x(gr/mm) $ \rho $y(gr/mm) (1,5) 0.48016 − 1.07329 1199.99228 1199.90331 (2,5) 0.48820 − 1.08118 1199.99563 1199.90466 (3,5) 0.48496 − 1.07812 1200.02361 1199.90413 (4,5) 0.48669 − 1.07981 1200.02964 1199.90443 (5,5) 0.48652 − 1.07963 1200.01899 1199.90439 (5,4) 0.48654 − 1.07839 1200.01872 1199.87662 (5,3) 0.48653 − 1.07917 1200.01889 1199.88735 (5,2) 0.48668 − 1.06947 1200.01681 1199.88468 (5,1) 0.48653 − 1.07342 1200.01767 1199.87282 Average value 0.48587 − 1.07694 1200.01469 1199.89360 Standard deviation 0.002158 0.003702 0.01171085 0.01322980 
下载: 导出CSV
Table 2. The results of the measurement of the 2D grating calibration area
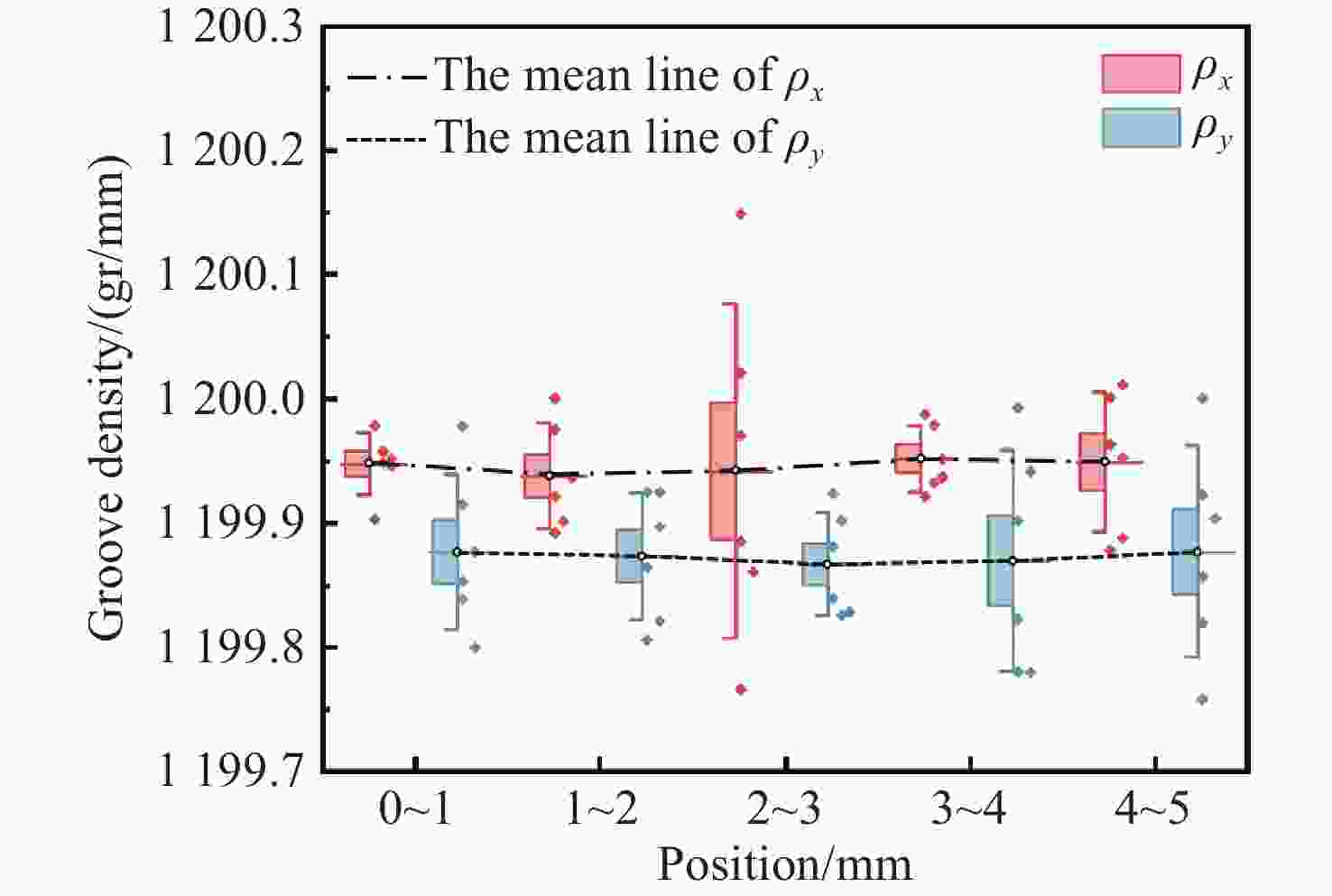
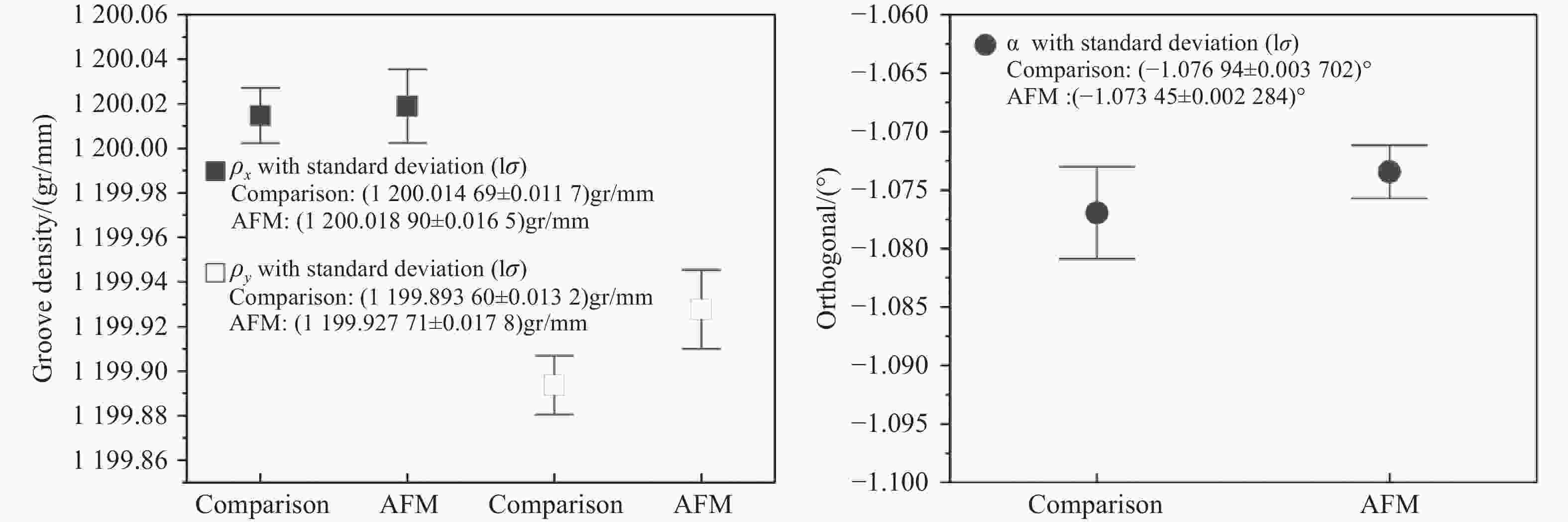
Measuring field α(°) $ \rho $x(gr/mm) $ \rho $y(gr/mm) 1 − 1.07126 1200.03871 1199.94367 2 − 1.07313 1199.99825 1199.92325 3 − 1.07493 1200.01830 1199.92155 4 − 1.07138 1200.00781 1199.94672 5 − 1.07653 1200.03141 1199.90339 Average value − 1.07345 1200.01890 1199.92771 Standard deviation 0.002284 0.016573373 0.017786239
下载: 导出CSV
-
[1] GAO W, KIM S W, BOSSE H, et al. Measurement technologies for precision positioning[J]. CIRP Annals, 2015, 64(2): 773-796. doi: 10.1016/j.cirp.2015.05.009 [2] TAN J B. Ultra-precision measurement and high-end equipment manufacturing quality[J]. China Industry & Information Technology, 2020(6): 18-23. (in Chinese) (查阅网上资料, 未找到本条文献英文翻译, 请确认). [3] BUTLER H. Position control in lithographic equipment: an enabler for current-day chip manufacturing[J]. IEEE Control Systems Magazine, 2011, 31(5): 28-47. doi: 10.1109/MCS.2011.941882 [4] WANG L J, ZHANG M, ZHU Y. Review of monomeric large-size and high precision holographic planar grating manufacturing technology[J]. Optics and Precision Engineering, 2021, 29(8): 1759-1768. (in Chinese). doi: 10.37188/OPE.20212908.1759 [5] WANG L J, ZHANG M, ZHU Y, et al. Review of ultra-precision optical interferential grating encoder displacement measurement technology for immersion lithography scanner[J]. Optics and Precision Engineering, 2019, 27(9): 1909-1918. (in Chinese). doi: 10.3788/OPE.20192709.1909 [6] AL-RAWASHDEH Y M, AL JANAIDEH M, HEERTJES M F. Kinodynamic generation of wafer scanners trajectories used in semiconductor manufacturing[J]. IEEE Transactions on Automation Science and Engineering, 2023, 20(1): 718-732. doi: 10.1109/TASE.2022.3196318 [7] LI X H, CUI C. Grating interferometric precision nanometric measurement technology[J]. Optics and Precision Engineering, 2024, 32(17): 2591-2611. (in Chinese). doi: 10.37188/OPE.20243217.2591 [8] ZHOU W Y, SUN Y J, LIU ZH W, et al. A random angle error interference eliminating method for grating interferometry measurement based on symmetry Littrow structure[J]. Laser & Photonics Reviews, 2025, 19(11): 2401659. [9] 冯灿. 平面位移测量用二维衍射光栅的标定方法[D]. 北京: 清华大学, 2012.FENG C. Calibration method of two-dimensional diffraction gratings used for planar displacement measurement[D]. Beijing: Tsinghua University, 2012. (in Chinese). [10] YACOOT A, KOENDERS L. Recent developments in dimensional nanometrology using AFMs[J]. Measurement Science and Technology, 2011, 22(12): 122001. doi: 10.1088/0957-0233/22/12/122001 [11] SHENG B, CHEN G H, HUANG Y SH, et al. Measurement of grating groove density using multiple diffraction orders and one standard wavelength[J]. Applied Optics, 2018, 57(10): 2514-2518. doi: 10.1364/AO.57.002514 [12] LEI L H, LIU Y, CHEN X, et al. Fast and accurate calibration of 1D and 2D gratings[J]. Advanced Materials Research, 2011, 317-319: 2196-2203. [13] KOROTKOV V I, PULKIN S A, VITUSHKIN A L, et al. Laser interferometric diffractometry for measurements of diffraction grating spacing[J]. Applied Optics, 1996, 35(24): 4782-4786. doi: 10.1364/AO.35.004782 [14] VITUSHKIN L F, ZEILIKOVICH I S, KOROTKOV V I, et al. High-precision measurements of the groove spacing of diffraction gratings using the interference diffractometer and study of the quality of diffraction gratings[J]. Optics and Spectroscopy, 1994, 77(1): 129-135. [15] ISRAEL W, TIEMANN I, METZ G, et al. An international length comparison at an industrial level using a photoelectric incremental encoder as transfer standard[J]. Precision Engineering, 2003, 27(2): 151-156. doi: 10.1016/S0141-6359(02)00192-7 [16] SAWABE M, MAEDA F, YAMARYO Y, et al. A new vacuum interferometric comparator for calibrating the fine linear encoders and scales[J]. Precision Engineering, 2004, 28(3): 320-328. doi: 10.1016/j.precisioneng.2003.11.007 [17] TIEMANN I, SPAETH C, WALLNER G, et al. An international length comparison using vacuum comparators and a photoelectric incremental encoder as transfer standard[J]. Precision Engineering, 2008, 32(1): 1-6. doi: 10.1016/j.precisioneng.2007.02.003 [18] KIM J A, KIM J W, PARK B C, et al. Measurement of microscope calibration standards in nanometrology using a metrological atomic force microscope[J]. Measurement Science and Technology, 2006, 17(7): 1792-1800. doi: 10.1088/0957-0233/17/7/018 [19] KIM J A, KIM J W, PARK B C, et al. Calibration of two-dimensional nanometer gratings using optical diffractometer and metrological atomic force microscope[J]. Proceedings of SPIE, 2005, 5879: 58790Z. doi: 10.1117/12.614786 [20] KIM J A, KIM J W, KANG C S, et al. Measurements of two-dimensional gratings using a metrological atomic force microscope with uncertainty evaluation[J]. International Journal of Precision Engineering and Manufacturing, 2008, 9(2): 18-22. [21] DIXSON R, ORJI N G, FU J, et al. Traceable atomic force microscope dimensional metrology at NIST[J]. Proceedings of SPIE, 2006, 6152: 61520P. doi: 10.1117/12.656803 [22] MISUMI I, GONDA S, KUROSAWA T, et al. Uncertainty in pitch measurements of one-dimensional grating standards using a nanometrological atomic force microscope[J]. Measurement Science and Technology, 2003, 14(4): 463-471. doi: 10.1088/0957-0233/14/4/309 [23] MELI F, THALMANN R. Long-range AFM profiler used for accurate pitch measurements[J]. Measurement Science and Technology, 1998, 9(7): 1087-1092. doi: 10.1088/0957-0233/9/7/014 [24] JORGENSEN J F, JENSEN C P, GARNAES J. Lateral metrology using scanning probe microscopes, 2D pitch standards and image processing[J]. Applied Physics A, 1998, 66(S1): S847-S852. [25] DAI G L, KOENDERS L, POHLENZ F, et al. Accurate and traceable calibration of one-dimensional gratings[J]. Measurement Science and Technology, 2005, 16(6): 1241-1249. doi: 10.1088/0957-0233/16/6/001 [26] MISUMI I, GONDA S, KUROSAWA T, et al. Submicrometre-pitch intercomparison between optical diffraction, scanning electron microscope and atomic force microscope[J]. Measurement Science and Technology, 2003, 14(12): 2065-2074. doi: 10.1088/0957-0233/14/12/004 [27] EVES B J, PEKELSKY J R, DECKER J E. Uncertainty evaluation of the NRC imaging diffractometer[J]. Measurement Science and Technology, 2008, 19(7): 075103. doi: 10.1088/0957-0233/19/7/075103 [28] MELI F, THALMANN R, BLATTNER P. High precision pitch calibration of gratings using laser diffractometry[C]. Proceedings of 1st International Conference on Precision Engineering and Nanotechnology, 1999: 252-255. (查阅网上资料, 未找到本条文献出版者信息, 请确认并补充). [29] DAI G L, POHLENZ F, DZIOMBA T, et al. Accurate and traceable calibration of two-dimensional gratings[J]. Measurement Science and Technology, 2007, 18(2): 415-421. doi: 10.1088/0957-0233/18/2/S13 [30] NOBACH H, DAMASCHKE N, TROPEA C. High-precision sub-pixel interpolation in particle image velocimetry image processing[J]. Experiments in Fluids, 2005, 39(2): 299-304. doi: 10.1007/s00348-005-0999-z [31] WOO W H, YEN K S. Moiré fringe center determination using artificial neural network[J]. Proceedings of SPIE, 2015, 9631: 96312B. [32] GARNAES J, DIRSCHERL K. NANO5—2D grating—final report[J] Metrologia, 2008, 45(1A): 04003. [33] FENG C, KAJIMA M, GONDA S, et al. Accurate measurement of orthogonality of equal-period, two-dimensional gratings by an interferometric method[J]. Metrologia, 2012, 49(3): 236-244. doi: 10.1088/0026-1394/49/3/236 [34] XIE Y F, JIA W, ZHAO D, et al. Traceable and long-range grating pitch measurement with picometer resolution[J]. Optics Communications, 2020, 476: 126316. doi: 10.1016/j.optcom.2020.126316 [35] HSU C C, TSAI C M, YE CH Y, et al. Period measurement of a periodic structure by using a heterodyne grating interferometer[J]. Applied Optics, 2024, 63(15): 4211-4218. doi: 10.1364/AO.521993 [36] DONG X Y, SUN SH H, CUI J Y, et al. Error analysis of two-dimensional grating calibration system based on orthogonal dual-axis laser interferometer[J]. Acta Metrologica Sinica, 2019, 40(6A): 36-41. (in Chinese). [37] BIRCH K P, DOWNS M J. An updated Edlén equation for the refractive index of air[J]. Metrologia, 1993, 30(3): 155-162. doi: 10.1088/0026-1394/30/3/004 -
下载:
计量
- 文章访问数: 24
- HTML全文浏览量: 5
- PDF下载量: 0
- 被引次数: 0
