基于缩放卷积的瑞利-索末菲衍射积分的独立采样与补长方法
Independent sampling and padding for Rayleigh–Sommerfeld diffraction: A scaled convolution approach
doi: 10.37188/CO.EN-2025-0028
-
摘要:
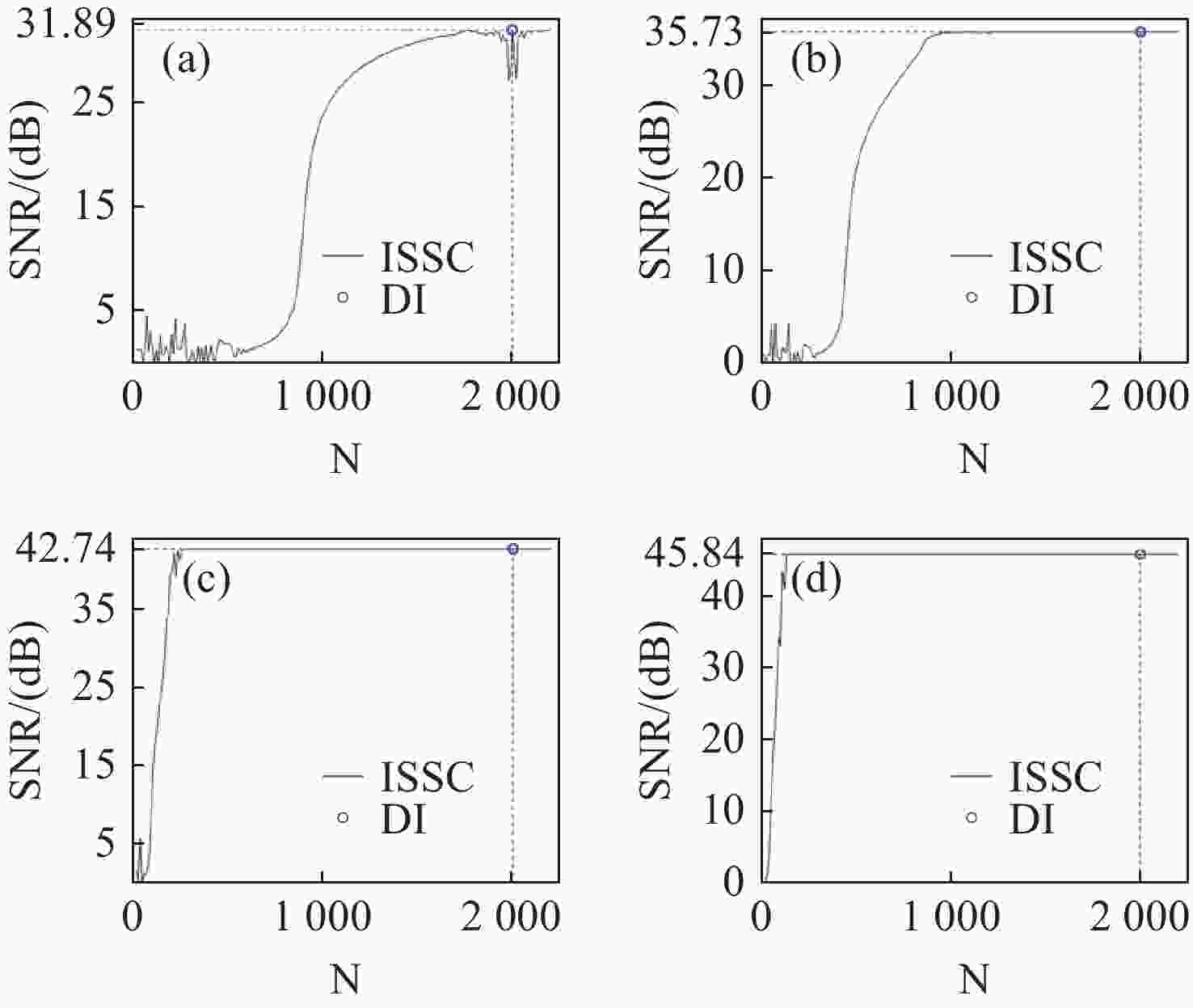
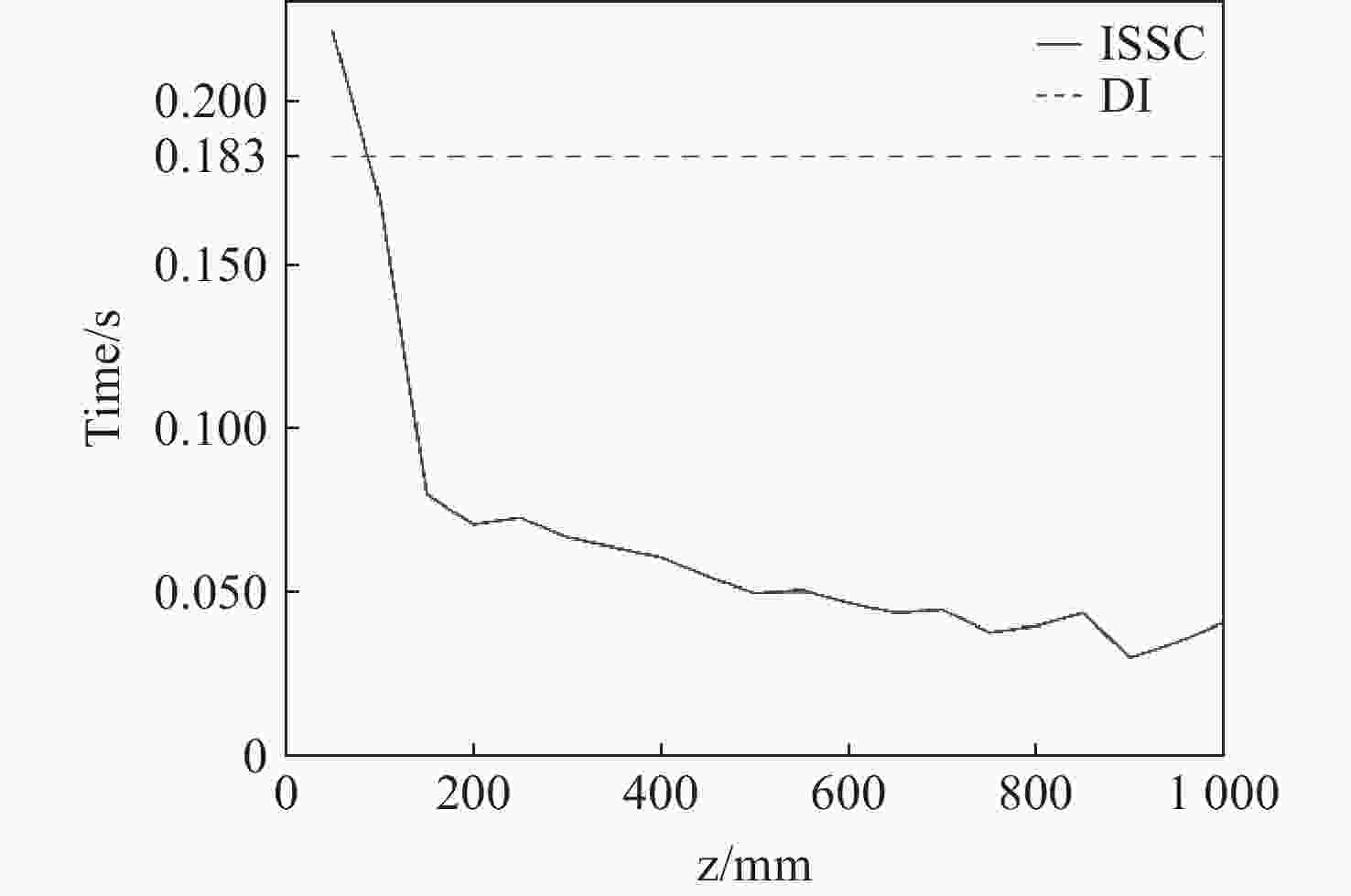
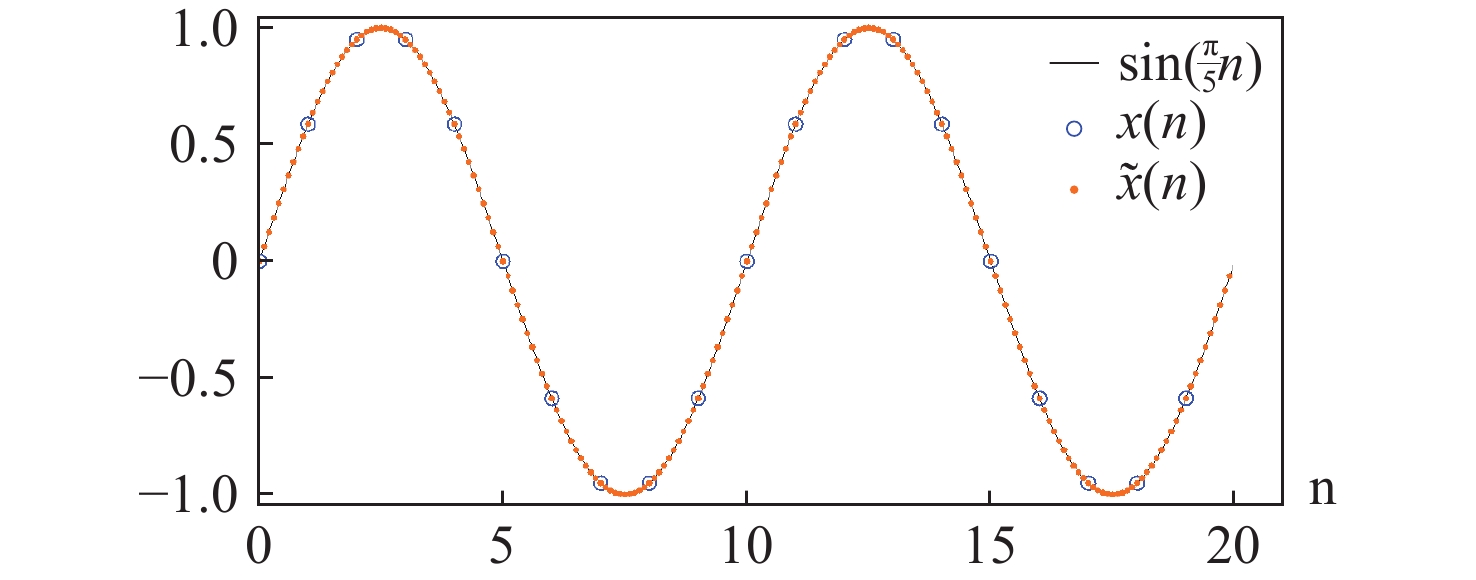
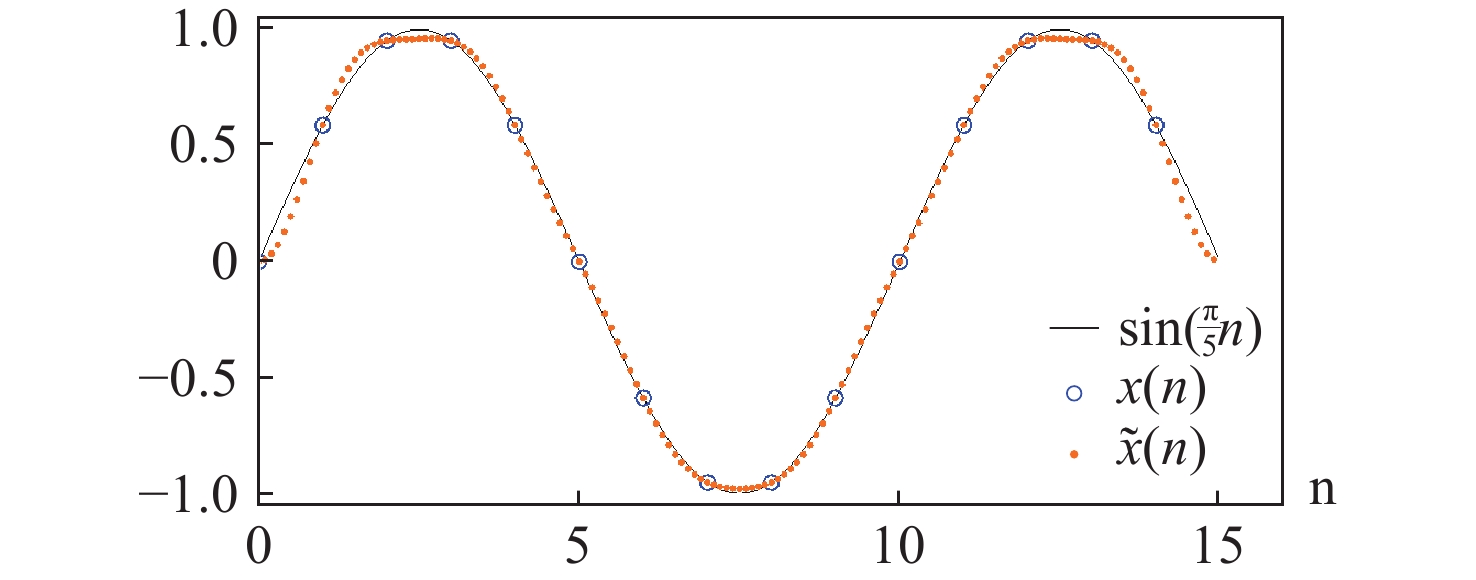
我们提出了一种新颖的对瑞利-索末菲衍射积分的快速数值计算方法，该方法在已有的缩放卷积方法的基础上发展而来。该方法实现了对离轴且输入面和观察面的采样间隔与采样数量均不等的一般情形的快速计算，并且可以任意调整脉冲响应函数的采样间隔从而实现对计算负载与计算精度的手动取舍。这种与插值等价的方法的误差主要来自脉冲响应函数的采样矩阵在其周期延拓边界上的不连续性，我们针对这一点提出了补长函数的概念及其构造方法，并评估了补长函数对提高计算精度的效果。通过数值模拟验证了所提出方法的可行性，并在简化场景里与直接积分法作了对比，表明所提出方法在非近场衍射下对输入面与观察面采样间隔不等的一般情形具有良好的计算精度，且在衍射距离很大时，虽然其计算精度无法超过直接积分法，但可以在几乎不影响计算精度的前提下，大幅降低计算量。该方法为计算全息等领域提供了在非近场情形下较为通用的衍射数值计算方法。
Abstract:We propose a novel fast numerical calculation method for the Rayleigh–Sommerfeld diffraction integral, which is developed based on the existing scaled convolution method. This approach enables fast calculations for general cases of off-axis scenarios where the sampling intervals and numbers of the input and observation planes are unequal. Additionally, it allows for arbitrary adjustment of the sampling interval of the impulse response function, facilitating a manual trade-off between computational load and accuracy. The errors associated with this method, which is equivalent to interpolation, primarily arise from the discontinuities of the sampling matrix of the impulse response function on its boundaries of periodic extension. To address this issue, we propose the concept of the padding function and its construction method, and we evaluate its effectiveness in enhancing computational accuracy. The feasibility of the proposed method is verified by numerical simulation and compared with the DI-method in a simplified scenario. It shows that the proposed method has good computational accuracy for the general case where the sampling interval of the input and observation plane is not equal under non-near-field diffraction, and when the diffraction distance is large, although the computational accuracy of the proposed method cannot exceed that of the DI-method, the computational amount can be significantly reduced with almost no effect on the computational accuracy. This method provides a general numerical calculation scheme of diffraction in the non-near field case for areas such as computational holography.
-
Key words:
- Rayleigh-Sommerfeld diffraction /
- scaled convolution /
- padding function
-
Figure 4. Real part of periodic extension of (a)
$ \left[h\right] $ before padding, (b)$ \left[{h}'\right] $ after padding
Figure 7. Numerical diffraction patterns at different magnifications, where: (a) reference image calculated by numerical integration for mag=20, while (b) mag=1, (c) mag=5, (d) mag=20 are calculated by ISSC
Figure 8. SNR of numerical diffraction with different oversampling factors and padding factors when
$ \textit{z} = $ $ 100 $ mm
Figure 10. SNR of the ISSC method varying with the sampling number of the IRF at a propagation distance of (a)
$ \textit{z} =50 $ mm, (b)$ \textit{z} =100 $ mm, (c)$ \textit{z} = $ $ 500 $ mm, and (d)$ \textit{z} =1\;000 $ mm
Figure 11. Average computation time of ISSC method varying with the propagation distance
Figure 12. Analytical curve, original signal x(n), and interpolated signal
$ \tilde{x}\left(n\right) $ for$ N=20 $ 
Figure 13. Analytical curve, original signal x(n), and interpolated signal
$ \tilde{x}\left(n\right) $ for$ {N}'=15 $ -
[1] GOODMAN J W. Introduction to Fourier Optics[M]. 3rd ed. Greenwoood Village, Co.: Roberts & Company Publishers, 2005. [2] PENG Y F, CHOI S, KIM J, et al. Speckle-free holography with partially coherent light sources and camera-in-the-loop calibration[J]. Science Advances, 2021, 7(46): eabg5040. doi: 10.1126/sciadv.abg5040 [3] FRATZ M, SEYLER T, BERTZ A, et al. Digital holography in production: an overview[J]. Light: Advanced Manufacturing, 2021, 2(3): 283-295. [4] BOOMINATHAN V, ROBINSON J T, WALLER L, et al. Recent advances in lensless imaging[J]. Optica, 2022, 9(1): 1-16. doi: 10.1364/OPTICA.431361 [5] XIAO J SH, ZHANG W H, ZHANG H. Sampling analysis for Fresnel diffraction fields based on phase space representation[J]. Journal of the Optical Society of America A, 2022, 39(2): A15-A28. doi: 10.1364/JOSAA.440464 [6] ZHANG W H, ZHANG H, JIN G F. Single-Fourier transform based full-bandwidth Fresnel diffraction[J]. Journal of Optics, 2021, 23(3): 035604. doi: 10.1088/2040-8986/abdf68 [7] MATSUSHIMA K, SHIMOBABA T. Band-limited angular spectrum method for numerical simulation of free-space propagation in far and near fields[J]. Optics Express, 2009, 17(22): 19662-19673. doi: 10.1364/OE.17.019662 [8] WEI H Y, LIU X, HAO X, et al. Modeling off-axis diffraction with the least-sampling angular spectrum method[J]. Optica, 2023, 10(7): 959-962. doi: 10.1364/OPTICA.490223 [9] ZHANG W H, ZHANG H, MATSUSHIMA K, et al. Shifted band-extended angular spectrum method for off-axis diffraction calculation[J]. Optics Express, 2021, 29(7): 10089-10103. doi: 10.1364/OE.419096 [10] SHEN F B, WANG A B. Fast-Fourier-transform based numerical integration method for the Rayleigh–Sommerfeld diffraction formula[J]. Applied Optics, 2006, 45(6): 1102-1110. doi: 10.1364/AO.45.001102 [11] LOBAZ P. Reference calculation of light propagation between parallel planes of different sizes and sampling rates[J]. Optics Express, 2011, 19(1): 32-39. doi: 10.1364/OE.19.000032 [12] ZHAO W L, LU J, MA J, et al. Technique for enhancing the accuracy of the Rayleigh–Sommerfeld convolutional diffraction through the utilization of independent spatial sampling[J]. Optics Letters, 2024, 49(5): 1385-1388. doi: 10.1364/OL.509688 [13] NASCOV V, LOGOFĂTU P C. Fast computation algorithm for the Rayleigh-Sommerfeld diffraction formula using a type of scaled convolution[J]. Applied Optics, 2009, 48(22): 4310-4319. doi: 10.1364/AO.48.004310 [14] ISSC-method-for-RSD-integration[EB/OL]. https://github.com/Alen-Yng/ISSC-method-for-RSD-integration. (查阅网上资料,未找到本条文献作者和更新日期和引用日期信息,请确认补充). -
下载:
计量
- 文章访问数: 25
- HTML全文浏览量: 7
- PDF下载量: 1
- 被引次数: 0
